Korelacje giełdowe - temat rzeka. Wśród inwestorów krąży wiele obiegowych opinii na ich temat, a fakt, że indeks WIG jest ujemnie skorelowany z parą walutową USD/PLN jest traktowany niemal dogmatycznie. Jakie jest jednak konkretne powiązanie poszczególnych spółek z tą parą rynku FX? Jak silne? Jak je mierzyć? Jakich błędów unikać? Podjęliśmy się zbadania tego zagadnienia, a poszczególne kroki i spostrzeżenia opisujemy w tym artykule. Wpierw podajemy podbudowę teoretyczną (ale i praktyczną!) do badań korelacji. Czytelnika niezainteresowanego poszczególnymi krokami i zależnościami odsyłamy do dalszej części tekstu.
Już na wstępie należy przytoczyć mantrę każdego statystyka - otóż korelacja to nie przyczynowość. O korelacji w kontekście giełdowym mówimy, gdy notowania pary walorów poruszają się na ogół względem siebie w zadanym kierunku. Jeśli korelacja jest dodatnia, wzrostom na jednym walorze odpowiadają zazwyczaj wzrosty na drugim. W przypadku korelacji ujemnej zależność jest odwrotna. To znaczy, że gdy jedna spółka rośnie, druga spada. Widzimy zatem, że korelacja dotyczy samych ruchów cenowych, nie interesują nas ich przesłanki czy podłoże. Równie dobrze może ich w ogóle nie być. Przyczynowość nie dopuszcza takiej możliwości, stwierdzając, że “A wynika z B”. Najodpowiedniejszą strategią byłoby zatem identyfikowanie zależności na gruncie przyczynowości, jak chociażby wzrost cen miedzi tworzący fundamentalną przesłankę do wzrostu notowań KGHM-u.
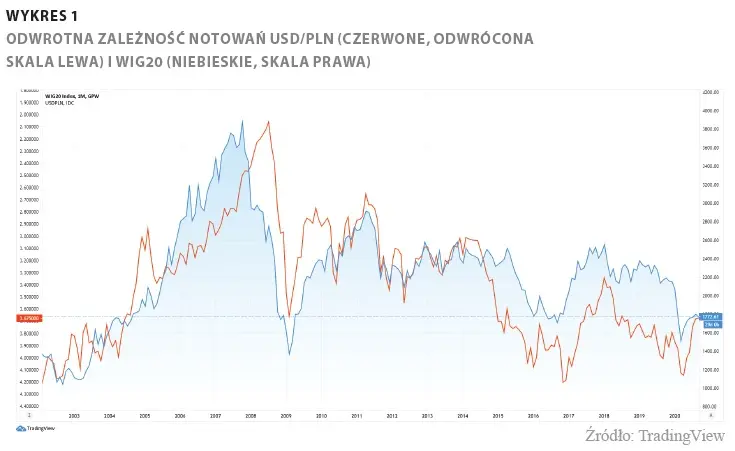
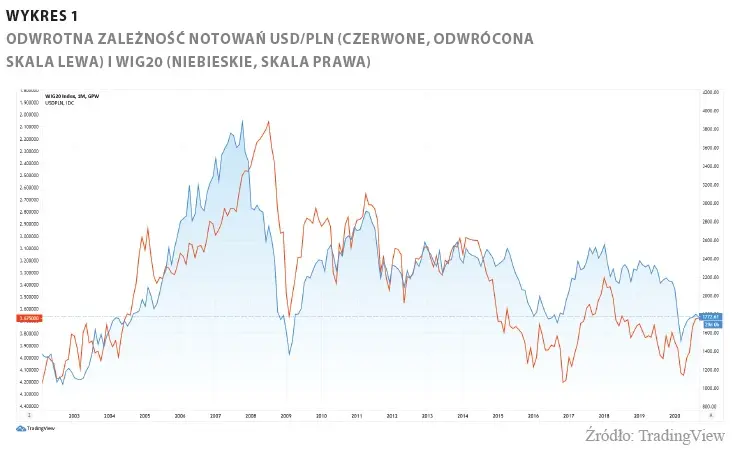
Warto zdać sobie sprawę, że korelacje na rynkach finansowych nie są stałe oraz różnią się swoją siłą. Z tego pierwszego wynika, że nie należy badać korelacji w ujęciu - dajmy na to - 20 lat notowań, ponieważ mogła się ona już zwyczajnie zdezaktualizować, a wcześniejsze wyniki zaburzają aktualny odczyt. Trzeba nam zatem zastosować ruchome okno statystyczne, działające na zasadzie średniej ruchomej. Przykładowo możemy założyć (jak w prezentowanych niżej badaniach), że interesuje nas korelacja 750-sesyjna, czyli z grubsza 3-letnia. Uwzględniamy zatem zawsze 750 obserwacji - gdy przesuwamy się w czasie, najstarsze dane wypadają, a zastępują je nowe do obliczeń. Korelacja zatem stopniowo się zmienia wraz z zastępowaniem starszych danych nowszymi, co odzwierciedla postępujące zmiany na rynkach, które nigdy nie stoją w miejscu. Polecamy właśnie owe 750 okresów (sesji) na podstawie własnych badań. Utworzone w ten sposób szeregi czasowe korelacji traktowane jako funkcja są wystarczająco stabilne, by nie reagować skrajnie na krótkoterminowe zaburzenia rynkowe, a przy tym wystarczająco dynamiczne, by stopniowo w czasie zmieniać swój charakter.
Jak jednak mierzyć stopień korelacji? Statystyka proponuje co najmniej kilka rozwiązań. Bodaj najprostszym i najczęściej przytaczanym jest współczynnik korelacji Pearsona. Nie musisz znać jego wzoru, wystarczy, że w arkuszu kalkulacyjnym wybierzesz funkcję “=Pearson()” i zaznaczysz dwie odpowiednie serie danych (oczywiście o równej długości, czyli np. 750 wierszy każda). Na jakich danych jednak należy bazować? Na myśl większości inwestorów przychodzi od razu działanie na cenach zamknięcia z poszczególnych dni (można oczywiście rozpatrywać korelację w innych okresach, np. 5-minutowym, ale korelacja na interwale M5 nie musi się pokrywać z zależnościami na interwale dziennym). Jest to jednak zwodniczy pomysł, który prowadzić będzie do zafałszowanych wyników. Należy przyjąć, że ceny, a właściwie zmiany cen dwóch walorów, są ze sobą nieporównywalne w stosowanym wzorze. Najprostszym wytłumaczeniem jest tutaj skala zmian w ujęciu bezwzględnym - jak ma się zmiana ceny z 5 zł na 6 zł do zmiany z 800 zł na 960 zł?
Uważny czytelnik domyślił się już wniosku - musimy bazować na zmianach procentowych cen, które w przytoczonym przykładzie są sobie równe i wynoszą 20%. Sprowadzamy zatem owe “nieporównywalne” wielkościowo ceny do wspólnego mianownika procentowego. Sugerujemy przy tym pewną “sztuczkę”. Współczynnik korelacji Pearsona dotyczy wyłącznie korelacji liniowej. Odstępstwo od liniowości w naszych danych traktowane jest jako przejaw braku korelacji. Związek między zmianami cen walorów może być jednak nieliniowy, np. jak w funkcji kwadratowej (lub innej funkcji wielomianowej), czyli paraboliczny. Co wtedy? Proponujemy, by nie stosować prostych stóp zwrotu, a zwroty logarytmiczne. Wystarczy zastosować logarytm naturalny (funkcja “=ln()” w arkuszu kalkulacyjnym). Tak przygotowane szeregi przekazujemy do funkcji obliczającej współczynnik korelacji Pearsona. Ten ostatni przyjmuje wartości z zakresu od -1 do +1 włącznie. Minus 1 oznacza doskonałą korelację ujemną (czyli wzrost ceny jednego waloru = spadek ceny drugiego), a plus 1 - doskonałą dodatnią (wzrost ceny jednego waloru = wzrost drugiego). Jaką korelację możemy uznać za silną? Formalnie w dyskursie akademickim korelację za istotną przyjmuje się już od (-)0,2. Na potrzeby praktyki jednak z naszego doświadczenia byłoby to przynajmniej (-)0,5, a korelacja rzeczywiście przydatna byłaby od (-)0,7. Wyższą szkołą jazdy jest badanie poziomów statystycznej istotności (za pomocą tzw. wartości p), ponieważ może się okazać, że współczynnik korelacji jest wysoki, ale nieistotny statystycznie, a zatem nie można na jego podstawie stwierdzić występowania badanej zależności. Dodatkowo idealnie byłoby badać ową 750-okresową korelację na przestrzeni lat, czyli w ujęciu dynamicznym, stopniowo zbliżając się od najstarszych dostępnych notowań do chwili obecnej. W ten sposób otrzymuje się szereg zmian korelacji w czasie, przez co można ocenić jej stabilność. Dla pojedynczej spółki jest to zadanie wykonalne w godzinę, dla kilkunastu lub kilkuset - karkołomne bez znajomości języków programowania takich jak R czy Python.
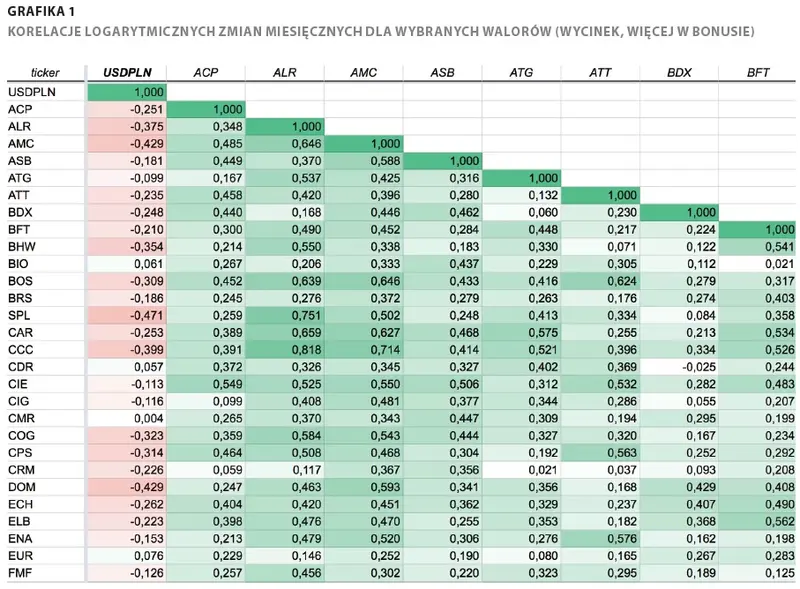
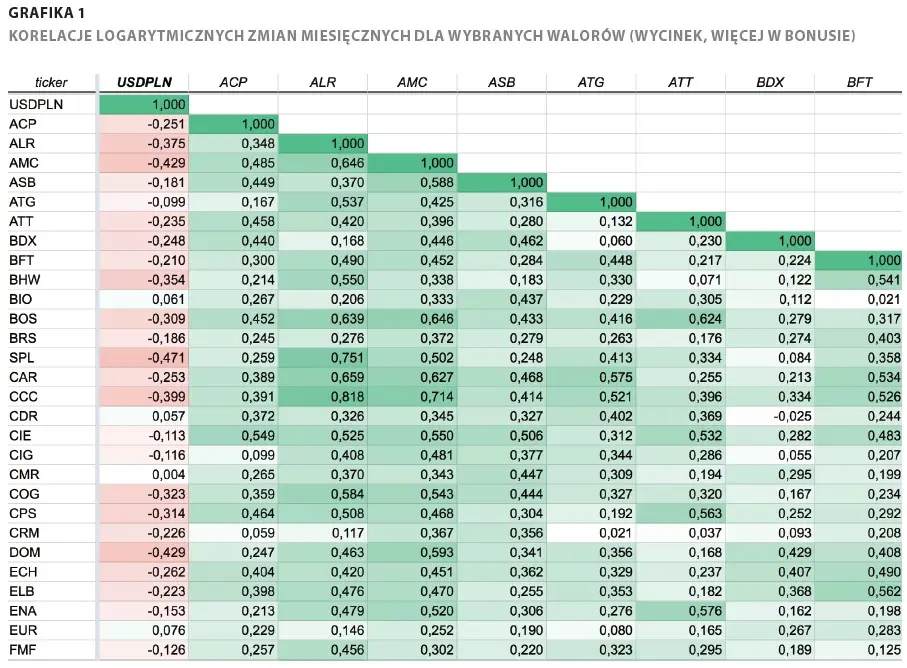
Wyposażeni w tę wiedzę możemy przystąpić do omawiania wyników. Wpierw pobraliśmy dzienne ceny zamknięcia wszystkich spółek z GPW, tak by poszczególne dni notowań pokrywały się z tymi dla WIG-u. W ten sposób odfiltrowaliśmy mniej płynne spółki i te, które nie miały z różnych względów kompletnej historii notowań. 750 sesji pokrywało zakres dat od 30 lipca 2017 r. do 25 sierpnia 2020 r., zaś liczba spółek spełniających kryteria wyniosła 86. Dołączyliśmy również szereg czasowy dla pary USD/PLN, która stanowiła clou analizy. Korelację badaliśmy na 4 poziomach: zmian dziennych, tygodniowych, miesięcznych i kwartalnych (oczywiście logarytmicznych). Zmiany powyżej tygodniowych wygładzają ewentualne opóźnienia, jakie mogą wystąpić między parami walorów. Co więcej, umożliwiają również badanie tzw. lagów statystycznych - w tym wypadku sprawdzaliśmy, czy przesunięcie zmian USD/PLN o jeden lub dwa okresy (tydzień, miesiąc, kwartał) do przodu ma wpływ na korelację. Innymi słowy, czy zachowanie się USD/PLN sprzed miesiąca czy kwartału rzutuje na notowania spółki obecnie (przeciwna zależność na zasadzie ruchów wyprzedzających spółki w stosunku do USD/PLN jest raczej nieprawdopodobna). Dlaczego by przy tym nie robić takich przesunięć dla zmian dziennych? Wykażą one najprawdopodobniej jedynie nieznaczny szum, ponieważ trudno oczekiwać, by dokładnie dana zmiana USD/PLN w tym samym dniu 2 miesiące temu znalazła swoje odzwierciedlenie akurat dzisiaj. Przy dłuższych okresach zmian jest to już sensowne, ponieważ walory, a raczej inwestorzy, mają czas, by odpowiednio zareagować. Logika jest tutaj następująca: inwestorzy stopniowo dyskontują przeszłe kształtowanie się kursu USD/PLN na wyniki spółki w danym okresie, które zostaną dopiero opublikowane.
Założyliśmy, że interesują nas jedynie rzeczywiście silne korelacje, tj. od poziomu (-)0,7. Znaleźliśmy ich z USD/PLN dokładnie trzy - jedynie wśród zmian kwartalnych. Okazuje się, że w ujęciu kwartalnym notowania GPW (jako spółki) są silnie dodatnio skorelowane (0,74) ze zmianami USD/PLN sprzed kwartału. W badanym okresie zatem wzrosty USD/PLN kwartał temu znajdowały odzwierciedlenie we wzrostach GPW w kwartale obecnym (i przeciwnie). Porównanie zmian kwartalnych obu walorów przedstawiamy na rysunku 3.
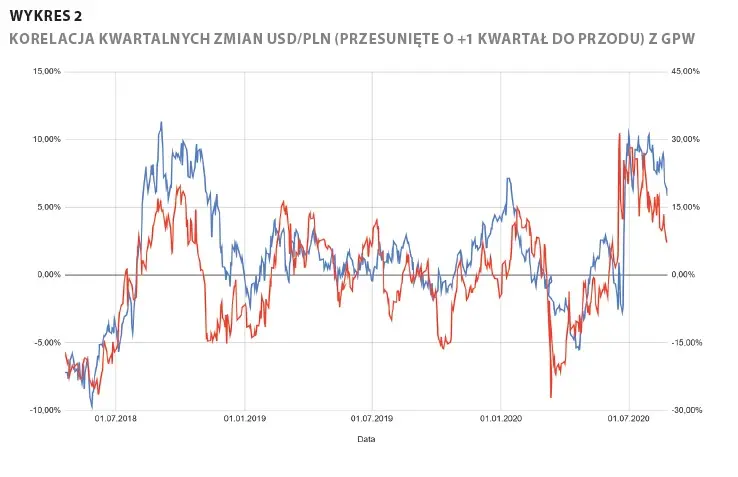
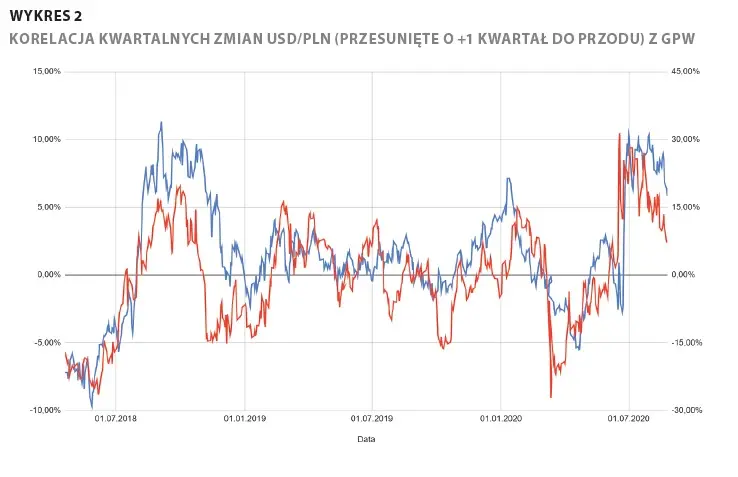
Dla rozpatrywanego przesunięcia kwartalnego o +1 silną korelację dodatnią (0,72) odnotowano także dla spółki Elemental (EMT) - była ona analogiczna do przedstawianej dla GPW. Co ciekawe, przy przesunięciu kwartalnym o +2 stanowcza większość obserwowanych korelacji dodatnich z arkusza prezentującego przesunięcie o +1 ulegała odwróceniu. Przykładowo dla GPW wynosiła -0,58, a dla Elementalu -0,52. Najsilniejsza wystąpiła dla Grupy ATM (ATG) i wyniosła -0,74. Oznacza to, że wzrosty USD/PLN dwa kwartały temu odnajdywały przeciętnie odzwierciedlenie w spadkach notowań ATG obecnie, co przedstawiono na rysunku 2.
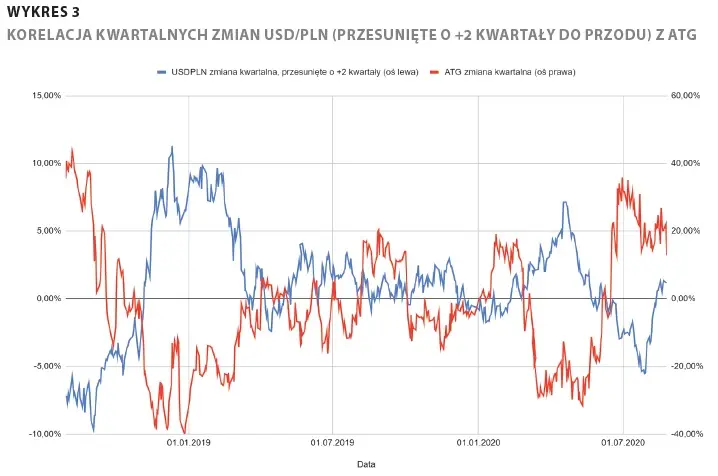
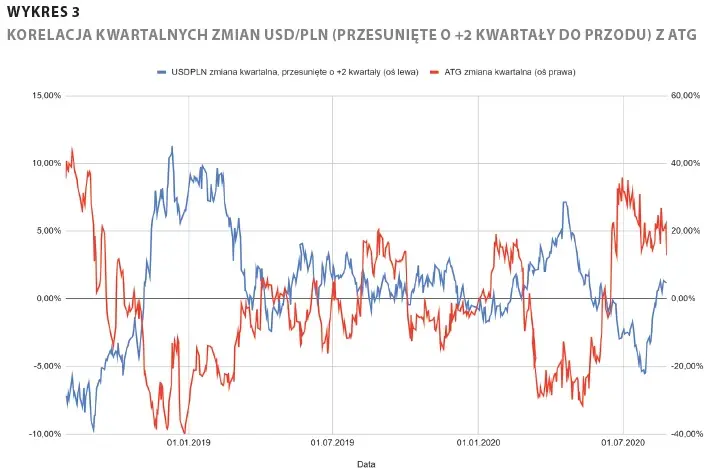
Mając wiedzę o określonych korelacjach przesuniętych w czasie, można, obserwując przykładowo kształtowanie się USD/PLN dziś, przewidywać, jak średnio mogą zachowywać się notowania GPW za kwartał. Nie zadziała to natomiast magicznie, natychmiastowo i nie będzie tak, że równo z minięciem kwartału notowania GPW nagle zaczną się kształtować w założony sposób. Warto zadać sobie również pytania o istnienie logicznych przesłanek dla istnienia danej zależności - jeśli je odnajdziemy, zwiększają one szansę, że nie jest to zwykły przypadek.
Na koniec bonus - podajemy link (także jako kod QR) do naszego arkusza z wynikami korelacji (jak na rysunku 1). W poszczególnych jego kartach uwzględniliśmy różne horyzonty zmian - od dziennych po kwartalne oraz przesunięcia w czasie notowań USD/PLN. Link: bit.ly/squaber-korelacje



